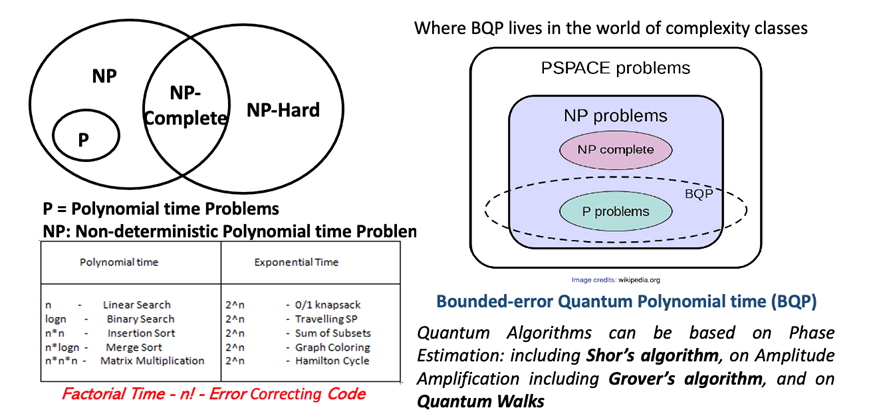
Per comprendere le prospettive del calcolo quantistico riferiamoci alla figura sottostante che illustra in modo concettualmente rigoroso e sintetico il rapporto tra calcolo quantistico e teoria della complessità computazionale (detta anche Ricerca Operativa), con particolare riferimento alle classi di problemi affrontabili in tempi polinomiali o esponenziali. Questo tema è centrale per comprendere in quali ambiti il quantum computing può offrire vantaggi concreti rispetto ai computer classici.
A sinistra sono presentati due insiemi principali. Il primo è quello dei problemi P, cioè risolvibili in tempo polinomiale da un algoritmo deterministico. Esempi tipici sono l’ordinamento, la ricerca binaria o la moltiplicazione di matrici: il tempo di esecuzione cresce al più come una potenza del numero di input. Allargando il campo, abbiamo i problemi NP, cioè risolvibili in tempo polinomiale da un algoritmo non deterministico, o equivalenti a problemi per cui, data una soluzione, è possibile verificarne la correttezza in tempo polinomiale. All’interno di NP si trovano i problemi NP-completi, come il problema dello zaino binario (knapsack), del commesso viaggiatore (Travelling Salesman Problem) o della colorazione dei grafi. Sono i problemi più difficili di NP, nel senso che se si trovasse un algoritmo polinomiale per risolverne anche uno solo, tutti gli altri diventerebbero risolvibili in modo efficiente.
Indice degli argomenti
Quantum Computing e Ricerca Operativa
La classe NP-hard comprende problemi almeno tanto difficili quanto quelli NP-completi, ma non necessariamente verificabili in tempo polinomiale. Le due rappresentazioni grafiche evidenziano come l’insieme P sia contenuto in NP, e come gli NP-completi siano una sottoclasse particolarmente critica dal punto di vista teorico e applicativo. In basso, una tabella riassume alcuni esempi di problemi con complessità polinomiale (come il merge sort o l’insertion sort) e altri con complessità esponenziale, i cui tempi di esecuzione crescono come due elevato a n o anche più velocemente. In calce, viene ricordato che problemi ancora più complessi, ad esempio nella codifica per la correzione degli errori, possono richiedere tempo fattoriale (n!), e sono quindi di fatto inaffrontabili con approcci classici.
La parte destra della figura introduce il concetto di BQP, cioè “Bounded-error Quantum Polynomial time”. Si tratta della classe di problemi risolvibili da un computer quantistico in tempo polinomiale, con un errore limitato e controllabile. La rappresentazione grafica mostra che BQP si colloca tra P e NP, ma non coincide né con l’una né con l’altra classe: contiene certamente alcuni problemi di P, ne affronta alcuni di NP, ma non si estende a tutti i problemi NP-completi. Inoltre, è contenuto nella classe PSPACE, che rappresenta l’insieme dei problemi risolvibili con uno spazio di memoria polinomiale. Questo schema aiuta a comprendere che il quantum computing non è una “macchina magica” capace di risolvere qualsiasi problema intrattabile, ma è una tecnologia molto promettente per una classe specifica di problemi computazionalmente ardui.
I problemi affrontabili in BQP sono legati ad algoritmi quantistici specifici, basati su tecniche come la stima della fase (phase estimation), l’amplificazione di ampiezza (amplitude amplification) e le camminate quantistiche (quantum walks). Tra gli algoritmi più noti rientra l’algoritmo di Shor, che consente di fattorizzare numeri interi molto grandi in tempo polinomiale, minando alla base la sicurezza dei sistemi crittografici tradizionali basati sull’algoritmo RSA (Rivest Shamir Adleman) che è il più usato oggi per le transazioni sicure su Internet. Un altro algoritmo fondamentale è quello di Grover, che consente di accelerare la ricerca non strutturata in un database, migliorandone l’efficienza da tempo lineare a tempo proporzionale alla radice quadrata del numero di elementi.
In sintesi, la figura riassume due concetti fondamentali. Il primo è la tassonomia dei problemi computazionali, e il secondo è il ruolo preciso e limitato, ma strategico, che i computer quantistici possono giocare nel risolverne una parte significativa. È proprio in ambiti come la crittografia, l’ottimizzazione combinatoria, la simulazione di sistemi quantistici e la chimica molecolare che il quantum computing potrà esprimere nei prossimi anni il suo potenziale trasformativo. La sfida scientifica e industriale è ora tradurre questa potenzialità in architetture stabili, algoritmi robusti e casi d’uso ad alto impatto.
La tabella sottostante offre un confronto diretto e sintetico tra supercomputer e computer quantistici, mettendo in evidenza le differenze fondamentali tra due paradigmi computazionali profondamente diversi. Si tratta di un confronto che non riguarda semplicemente la velocità o la potenza di calcolo, ma l’intero modello concettuale su cui ciascuna macchina si basa e le implicazioni pratiche in termini di applicazioni, vantaggi, limiti e direzioni di ricerca.
| FEATURE | SUPERCOMPUTER | QUANTUM COMPUTER |
| Computing Model | Bits that can be 0 or 1 | Qubits can be 0,1. Super-position of 0 and 1 |
| Processing Model | Parallel classical processing | Super-position & entanglement & interference |
| Strenghts | Deterministic calculations, large scale simulations | Solving specific problems exponentially faster |
| Weaknesses | Power intensive, scales linearly | Fragile qubits, high error rate |
| Best For | AI, physics simulation, weather modeling | Cryptography, optimization, life simulations |
| Challenges | Power consumption, scalability, data bottlenecks | Qubit de-coherence, noise, lack of fault tolerance |
| Current Research | Exa-scale (10^18) computing, neuro-morphic chips | Error correction, better qubits, hybrid quantum-classical approaches |
Confronto tra Supercomputer e Quantum Computer
Nel modello computazionale classico, che è quello adottato dai supercomputer, l’informazione è rappresentata da bit, che possono assumere valore 0 oppure 1, proprio come interruttori digitali. I calcoli avvengono in modo deterministico e sono eseguiti da processori che elaborano milioni o miliardi di operazioni per secondo, sfruttando l’elaborazione parallela. I supercomputer eccellono in compiti che richiedono simulazioni numeriche su larga scala, come la modellizzazione climatica, la simulazione di fenomeni fisici complessi o le applicazioni di intelligenza artificiale che si basano su deep learning. Il loro principale punto di forza è l’affidabilità e la capacità di produrre risultati ripetibili e verificabili.
Tuttavia, questi sistemi sono estremamente esigenti in termini energetici e le loro prestazioni crescono in modo sostanzialmente lineare: per raddoppiare la potenza di calcolo, serve in genere raddoppiare il numero di nodi o l’efficienza dei processori. Ciò implica sfide importanti in termini di consumo elettrico, dissipazione termica e scalabilità. La ricerca attuale nel campo dei supercomputer si concentra su due fronti principali: l’elaborazione exascale, cioè sistemi capaci di eseguire più di 10¹⁸ operazioni al secondo, e l’introduzione di architetture neuromorfiche, ispirate al funzionamento del cervello umano, per aumentare efficienza e flessibilità.
Il computer quantistico, al contrario, si fonda su un modello del tutto diverso. L’informazione è codificata nei qubit, unità quantistiche che possono essere contemporaneamente 0, 1 o una sovrapposizione di entrambi gli stati. Questo principio di sovrapposizione, insieme all’entanglement (cioè la correlazione quantistica tra qubit posti anche a grande distanza) e all’interferenza, consente di esplorare simultaneamente un numero enorme di possibili soluzioni a un problema. Ne consegue che un computer quantistico, per determinati tipi di problemi, può ottenere una velocità di calcolo esponenzialmente superiore rispetto ai computer classici.
La forza del calcolo quantistico risiede nella sua capacità di affrontare in modo efficiente problemi complessi come la fattorizzazione di numeri primi molto grandi (con implicazioni nella crittografia), l’ottimizzazione combinatoria, la simulazione di reazioni chimiche su scala atomica, la ricerca nei database non strutturati e la stima di probabilità nei sistemi dinamici. Tuttavia, i computer quantistici sono ancora in una fase embrionale. I qubit sono estremamente fragili, soggetti a fenomeni di de-coerenza, e i tassi di errore nelle operazioni sono ancora elevati. La mancanza di un’effettiva tolleranza agli errori e la difficoltà a mantenere stati quantistici coerenti per un tempo sufficiente sono le principali sfide tecnologiche attuali.
Per questo motivo, la ricerca nel campo dei quantum computer si concentra su tre fronti: miglioramento della qualità dei qubit, sviluppo di tecniche di correzione degli errori più efficienti e creazione di architetture ibride quantistico-classiche. In questi sistemi, il calcolo quantistico viene utilizzato solo per le parti più difficili di un problema, mentre il resto è gestito da hardware tradizionale, permettendo di ottenere vantaggi tangibili anche con macchine ancora limitate in termini di qubit utili.
In conclusione, supercomputer e computer quantistici non sono in competizione, ma rappresentano approcci complementari. I primi continueranno a essere insostituibili per simulazioni su larga scala e applicazioni di IA industriale, mentre i secondi si profilano come strumenti specializzati per affrontare classi di problemi altrimenti intrattabili. In futuro, potremmo vedere architetture integrate dove CPU (Central Processing Unit, GPU (Graphics Processing Unit), DPU (Data Processing Unit) e QPU (Quantum Processing Unit) collaborano sinergicamente per dare risposta ai crescenti bisogni computazionali della società digitale.











